JavaScript中的%(求余运算符)

在JavaScript中,除了加减乘除运算之外,还会存在求模运算,即求余数的运算,这种运算方式与数学中的求余运算是息息相关的,今天讲一下JavaScript中的求模运算(运算符为 % ).

在数学中,一个整数对另外一个整数做除法运算,如果不能够整除,我们可以用余数的形式表示,比如:

10 ÷ 3 = 3 ······ 1 (读法:10除以3等于3余1) 计算方式如图:

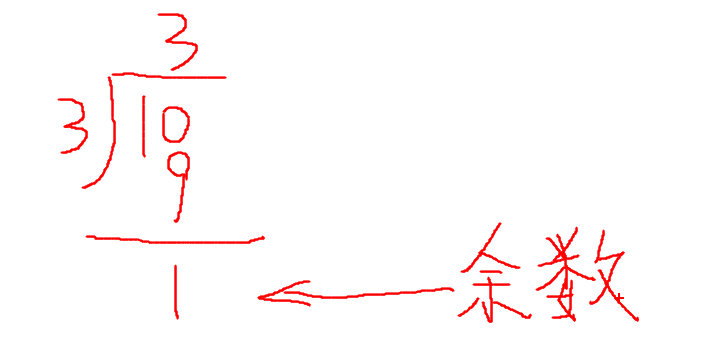
余数的性质:

1）余数和除数的差的绝对值要小于除数的绝对值（适用于实数域） 2）被除数 = 除数×商+余数

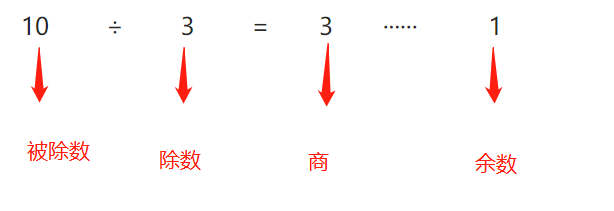
翻译一下:

1) 余数的绝对值不能比除数的绝对值大,比如在当前算式中,1是余数,÷号后的3是除数,1<3是合理的,如果余数的绝对值比除数绝对值大,证明还没有除尽

2) 被除数=除数×商+余数当前的算式中, 10 = 3 × 3 + 1

有了以上的概念之后,我们Js中的求模运算就比较容易理解了,求模运算是只返回余数的运算,比如:

10%3 => 1

(读作:10对3求模,返回1. 或10对3求余,返回1) 这里就不返回商了,只返回余数

那求模运算在程序中一般应用在什么地方呢?

一般是判断是否能整除,或者判断奇偶数时会用到

// 判断是否能整除案例
var num = 100
if(num % 4 == 0){
  console.log('num能够被4整除');
}else{
  console.log('num不能被4整除');
}

// 判断奇偶数案例(偶数:能被2整除   奇数:不能被2整除)
var num1 = 25
if(num1 % 2 == 0){
  console.log('num1是偶数');
}else{
  console.log('num1是奇数');
}